树 是一种经常用到的数据结构,用来模拟具有树状结构性质的数据集合。
树里的每一个节点有一个根植和一个包含所有子节点的列表。从图的观点来看,树也可视为一个拥有N个节点和N-1条边的一个有向无环图.
- 树结构中的常见用语:
- 节点的深度 - 从树的根节点到该节点的边数
- 节点的高度 - 该节点和叶子之间最长路径上的边数
- 树的高度 - 其根节点的高度
二叉搜索树
二叉搜索树(BST)是二叉树的一种特殊表示形式,它满足如下特性:
- 每个节点中的值必须大于(或等于)存储在其左侧子树中的任何值。
- 每个节点中的值必须小于(或等于)存储在其右子树中的任何值。
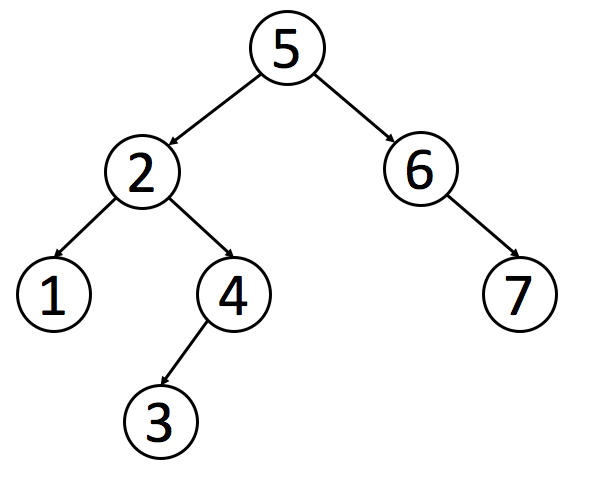
像普通的二叉树一样,我们可以按照前序、中序和后序来遍历一个二叉搜索树。 但是值得注意的是,对于二叉搜索树,我们可以通过中序遍历得到一个递增的有序序列。因此,中序遍历是二叉搜索树中最常用的遍历方法。
二叉搜索树的有优点是,即便在最坏的情况下,也允许你在O(h)的时间复杂度内执行所有的搜索、插入、删除操作。通常来说,如果你想有序地存储数据或者需要同时执行搜索、插入、删除等多步操作,二叉搜索树这个数据结构是一个很好的选择。
O(h) :h是树高度
对于二叉搜索树的每个节点来说,若其左子树共有m个节点,那么该节点是组成二叉搜索树的有序数组中第m + 1个值。
高度平衡的二叉搜索树
高度平衡的二叉搜索树是二叉搜索树的特殊表示形式,旨在提高二叉搜索树的性能。
一个高度平衡的二叉搜索树(平衡二叉搜索树)是在插入和删除任何节点之后,可以自动保持其高度最小。也就是说,有N个节点的平衡二叉搜索树,它的高度是logN。并且,每个节点的两个子树的高度不会相差超过1。
为什么是LogN呢?
下面是一个普通二叉搜索树和一个高度平衡的二叉搜索树的例子:
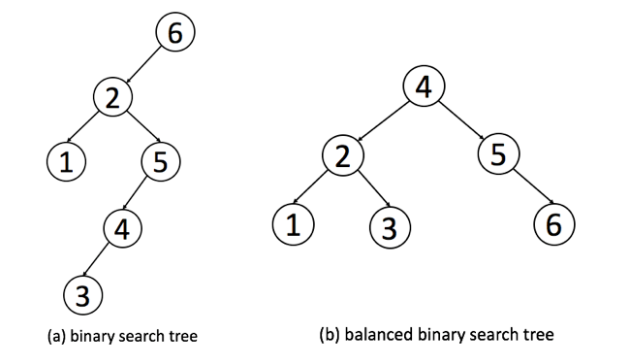
根据定义, 我们可以判断出一个二叉搜索树是否是高度平衡的 (平衡二叉树):
- 一个有N个节点的平衡二搜索叉树的高度总是logN。因此,我们可以计算节点总数和树的高度,以确定这个二叉搜索树是否为高度平衡的。
- 高度平衡的二叉树一个特性: 每个节点的两个子树的深度不会相差超过1。我们也可以根据这个性质,递归地验证树。
为什么需要用到高度平衡的二叉搜索树?
树的节点总数N和高度h之间的关系。 对于一个平衡二叉搜索树, 我们已经在前文中提过, h>=logN 。但对于一个普通的二叉搜索树, 在最坏的情况下, 它可以退化成一个链(只有单边子树)。
因此,具有N个节点的二叉搜索树的高度在logN到N区间变化。也就是说,搜索操作的时间复杂度可以从logN变化到N。这是一个巨大的性能差异。
高度平衡的二叉搜索树对提高性能起着重要作用。
如何实现一个高度平衡的二叉搜索树?
有许多不同的方法可以实现。尽管这些实现方法的细节有所不同,但他们有相同的目标:
- 采用的数据结构应该满足二分查找属性和高度平衡属性。
- 采用的数据结构应该支持二叉搜索树的基本操作,包括在
O(logN)时间内的搜索、插入和删除,即使在最坏的情况下也是如此。
常见的的高度平衡二叉树列表供您参考:
- 红黑树
- AVL树
- 伸展树
- 树堆
高度平衡的二叉搜索树的实际应用
高度平衡的二叉搜索树在实际中被广泛使用,因为它可以在O(logN)时间复杂度内执行所有搜索、插入和删除操作。
平衡二叉搜索树的概念经常运用在Set和Map中。 Set和Map的原理相似。
Set(集合)是另一种数据结构,它可以存储大量key(键)而不需要任何特定的顺序或任何重复的元素。 它应该支持的基本操作是将新元素插入到Set中,并检查元素是否存在于其中。
通常,有两种最广泛使用的集合:哈希集合(Hash Set)和树集合(Tree Set)。哈希集和树集之间的本质区别在于树集中的键是有序的。
红黑树
AVL树(自动平衡二叉搜索树)
伸展树
树堆
N叉树
N叉树的遍历: 对于每个子节点: 通过递归地调用遍历函数来遍历以该子节点为根的子树
// N叉树的节点定义
public class Node
{
public int val;
public IList<Node> children;
public Node()
{
}
public Node(int _val)
{
val = _val;
}
public Node(int _val, IList<Node> _children)
{
val = _val;
children = _children;
}
}
遍历主要是用foreach遍历children, 注意有时候需要反序.
N叉树的经典递归解法
- “自顶向下”的解决方案
“自顶向下”意味着在每个递归层次上,我们首先访问节点以获得一些值,然后在调用递归函数时,将这些值传给其子节点。
一个典型的 “自顶向下” 函数 top_down(root, params) 的工作原理如下:
1. 对于 null 节点返回一个特定值
2. 如果有需要,对当前答案 answer 进行更新 // answer <-- params
3. for each child node root.children[k]:
4. ans[k] = top_down(root.children[k], new_params[k]) // new_params <-- root.val, params
5. 如果有需要,返回答案 answer // answer <-- all ans[k]
- “自底向上”的解决方案
“自底向上” 意味着在每个递归层次上,我们首先为每个子节点递归地调用函数,然后根据返回值和根节点本身的值给出相应结果。
一个典型的 “自底向上” 函数 bottom_up(root) 的工作原理如下:
1.对于 null 节点返回一个特定值
2.for each child node root.children[k]:
3. ans[k] = bottom_up(root.children[k]) // 为每个子节点递归地调用函数
4. 返回答案 answer // answer <- root.val, all ans[k]
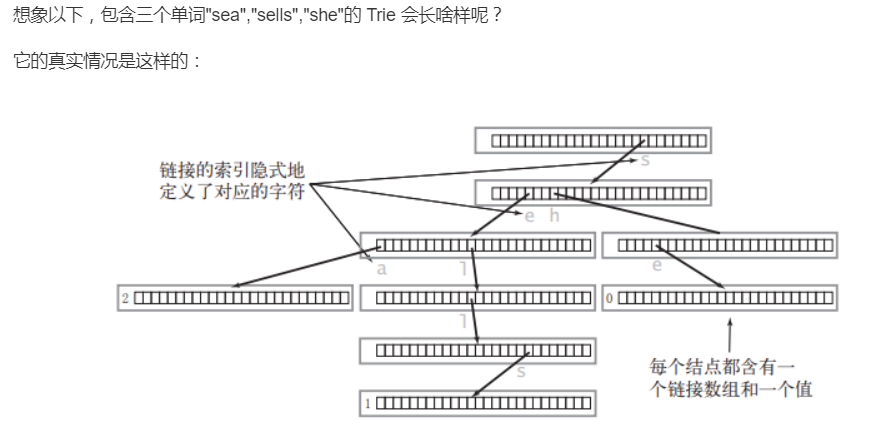
前缀树(字典树)
应用于: 自动补全, 拼写检查,IP路由(最长前缀匹配), T9 (九宫格) 打字预测,单词游戏等.
前缀树,又称字典树,是N叉树的特殊形式。
通常来说,一个前缀树是用来存储字符串的。前缀树的每一个节点代表一个字符串(前缀)。每一个节点会有多个子节点,通往不同子节点的路径上有着不同的字符。子节点代表的字符串是由节点本身的原始字符串,以及通往该子节点路径上所有的字符组成的。
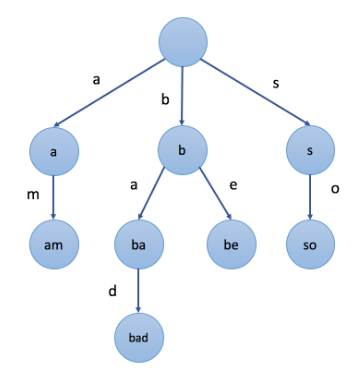
在上图示例中,我们在节点中标记的值是该节点对应表示的字符串。例如,我们从根节点开始,选择第二条路径 ‘b’,然后选择它的第一个子节点 ‘a’,接下来继续选择子节点 ‘d’,我们最终会到达叶节点 “bad”。节点的值是由从根节点开始,与其经过的路径中的字符按顺序形成的。
值得注意的是,根节点表示空字符串。
前缀树的一个重要的特性是,节点所有的后代都与该节点相关的字符串有着共同的前缀。这就是前缀树名称的由来。
例如,以节点 “b” 为根的子树中的节点表示的字符串,都具有共同的前缀 “b”。反之亦然,具有公共前缀 “b” 的字符串,全部位于以 “b” 为根的子树中,并且具有不同前缀的字符串来自不同的分支。
前缀树有着广泛的应用,例如自动补全,拼写检查等等。我们将在后面的章节中介绍实际应用场景。
如何表示一个前缀树
- 第一种方法是用数组存储子节点。
public static final int N = 26;
public TrieNode[] children = new TrieNode[N];
root.children[c - 'a'];
但并非所有的子节点都需要这样的操作,所以这可能会导致空间的浪费。
- 使用 Hashmap 来存储子节点。
public HashMap<char, TrieNode> children = new HashMap<char, TrieNode>();
节省了空间。这个方法也更加灵活,因为我们不受到固定长度和固定范围的限制。
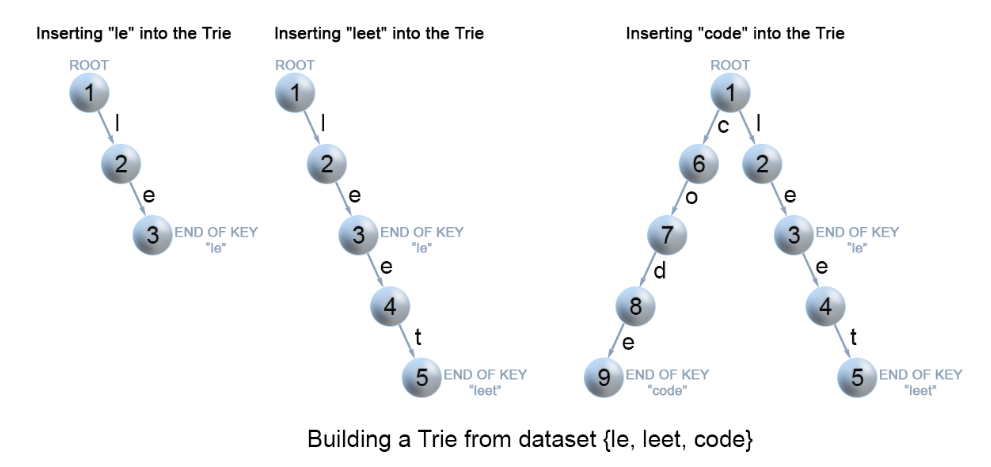
前缀树的插入
向 Trie 树中插入键
我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况:
- 链接 存在。 沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
- 链接 不存在。创建一个新的节点,并将它与父节点的链接相连,该链接与当前的键字符相匹配。
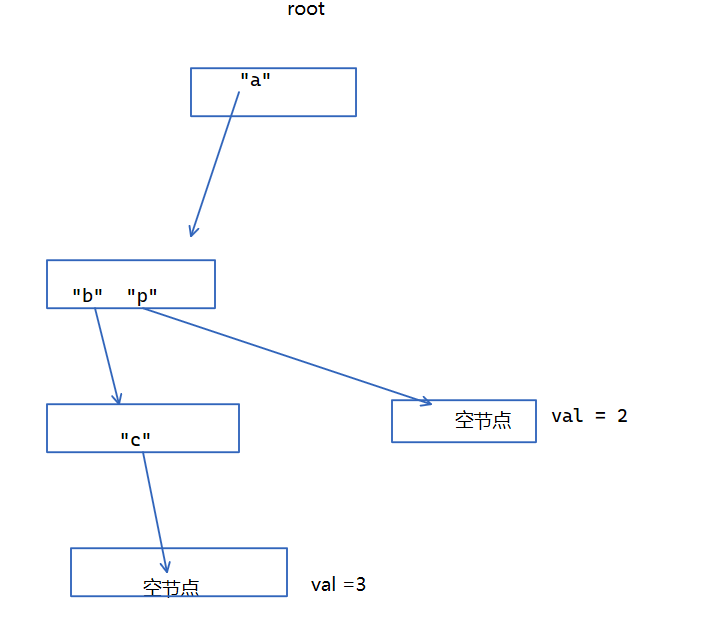
例题
- 677.键值映射
- 648.单词替换 (附带用哈希表算法的比较)
s.Insert("abc", 3);
s.Insert("ap", 2);
s.Sum("a");
前缀树结构模板
// 时间复杂度:
// 如果单词的最长长度为N,则Trie的高度为N + 1。
// 因此,所有insert、search和startsWith方法的时间复杂度为O(N)。
//
// 空间复杂度:
// 如果我们总共要插入M个单词,且单词的长度最多为N,那么在最坏的情况下,最多将有M*N个节点(任何两个单词都没有公共前缀)。
// 我们假设最大有K个不同的字符(在这个问题中K等于26,但是在不同的情况下可能不同)。因此,每个节点将维护一个最大为K的映射。
// 因此,空间复杂度为O(M*N*K)。
public class TrieNode
{
public TrieNode() => dic = new Dictionary<char, TrieNode>();
/// <summary>
/// 维护节点中的字典, 字符和对应的节点(连线)
/// </summary>
private Dictionary<char, TrieNode> dic;
/// <summary>
/// 是否是单词末尾
/// </summary>
private bool isEnd;
/// <summary>
/// 节点中的字典是否存在ch这个字符对应连接的下一个节点
/// </summary>
public bool ContainsKey(char ch) => dic.ContainsKey(ch);
/// <summary>
/// 获取字符对应连接的下一个节点
/// </summary>
public TrieNode Get(char ch) => dic[ch];
/// <summary>
/// 放入字符和对应连接的下一个节点
/// </summary>
public void Put(char ch, TrieNode node) => dic[ch] = node;
/// <summary>
/// 设置单词结束
/// </summary>
public void SetEnd() => isEnd = true;
/// <summary>
/// 返回是否是一个完整单词
/// </summary>
public bool IsEnd() => isEnd;
}
// 减少空间浪费, 使用字典,而不是固定长度的数组
public class Trie
{
private TrieNode root;
/** Initialize your data structure here. */
public Trie()
{
root = new TrieNode();
}
/// <summary>
/// 往前缀树插入单词
/// </summary>
public void Insert(string word)
{
TrieNode node = root;
for (int i = 0; i < word.Length; i++)
{
char currentChar = word[i];
// 填充根节点对应字符的子节点
if (!node.ContainsKey(currentChar))
{
node.Put(currentChar, new TrieNode());
}
// 进入该字符的子节点, 迭代下一个字符
// 沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
node = node.Get(currentChar);
}
// 遍历完此单词设置标志位flag
node.SetEnd();
}
/// <summary>
/// 搜索前缀,返回最后一个字符连接的下一个节点
/// </summary>
private TrieNode SearchPrefix(String word)
{
TrieNode node = root;
for (int i = 0; i < word.Length; i++)
{
char currentChar = word[i];
if (node.ContainsKey(currentChar))
{
node = node.Get(currentChar);
}
else
{
return null;
}
}
return node;
}
/// <summary>
/// 是否包含单词(标有End结尾)
/// </summary>
public bool Search(string word)
{
var node = SearchPrefix(word);
// 需要判断是否设置了单词结束的标志位
return node != null && node.IsEnd();
}
/// <summary>
/// 如果trie中有任何以给定前缀开头的单词,则返回true
/// </summary>
public bool StartsWith(string prefix)
{
TrieNode node = SearchPrefix(prefix);
// 不需要检查IsEnd, 只是搜索前缀,
return node != null;
}
}
您也可以通过数组来实现它,它将获得稍好一点的时间性能,但稍差一点的空间性能。
为什么不直接用哈希表?
您可能想知道为什么不使用哈希表来存储字符串。让我们对这两个数据结构做一个简短的比较。我们假设有N个键,一个键的最大长度是M。
- 时间复杂度
在哈希表中搜索的时间复杂度一般为O(1),但在最坏的情况下,如果冲突太多,我们使用高度平衡BST(比如SortedDiconary)来解决冲突,则时间复杂度为O(logN)。
在前缀树中搜索的时间复杂度为O(M)。
哈希表在大多数情况下都是赢家。
- 空间复杂度
哈希表 的空间复杂度为O(M * N),如果希望哈希表具有与Trie相同的功能,可能需要存储多个key副本。例如,您可能希望存储一个关键字“apple”的“a”、“ap”、“app”、“appl”和“apple”,以便通过前缀进行搜索。在这种情况下,空间复杂性可能会更大。
前缀树 的空间复杂度为O(M * N)。但实际上比估计的要小得多,因为在实际情况中会有很多单词有类似的前缀。
大多数情况下,前缀树是赢家。

