滑动窗口
- 3无重复字符的最长子串
- 209长度最小的子数组
双指针
- 26删除排序数组中的重复项
- 27移除元素
- 28实现strStr()
- 209长度最小的子数组
不仅适用于数组问题,而且还适用于链表问题。
// 双指针模板
// 获取空节点的下一个节点将导致空指针错误。例如,在我们运行 fast = fast.next.next 之前,需要检查 fast 和 fast.next 不为空。
ListNode slow = head;
ListNode fast = head;
while (slow != null && fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) { /
return true;
}
}
return false;
快慢指针
- 82删除排序链表中的重复元素 II
- 快乐数
不仅适用于数组问题,而且还适用于链表问题。
栈
- 20有效的括号
- 扁平化多级双向链表
链表
- 21合并两个有序链表
- 83删除排序链表中的重复元素
- 扁平化多级双向链表
二分查找
- 35搜索插入的位置
- 69x的平方根
动态规划
- 53最大子序和
- 70爬楼梯
- 494目标和
取决于该问题是否能用动态规划解决的是这些”小问题“会不会被被重复调用。
答:可以使用动态规划的问题一般都有一些特点可以遵循。 如题目的问法一般是 三种方式:
1.求最大值/最小值
2.求可不可行
3.求方案总数
如果你碰到一个问题,是问你这三个问题之一的,那么有90%的概率是使用动态规划来求解。
要重点说明的是,如果一个问题让你求出“所有的”方案和结果,则肯定不是使用动态规划。
分治法
- 53最大子序和
- 69x的平方根
牛顿迭代法的应用: 一个是求方程的根,另一个是求解最优化问题
查并集
- 200岛屿数量
- 547朋友圈(未做)
- 733图像渲染
- 1020飞地的数量(未做)
- 1254统计封闭岛屿的数目(未做)
桶排序
- 220存在重复元素III
我们有 8 个未排序的整数。我们首先来创建五个桶,这五个桶分别包含 [0,9], [10,19], [20, 29], [30, 39], [40, 49]这几个区间。这 8 个元素中的任何一个元素都在一个桶里面。对于值为 x 的元素来说,它所属桶的标签为 x/w,在这里我们让 w = 10。对于每个桶我们单独用其他排序算法进行排序,最后按照桶的顺序收集所有的元素就可以得到一个有序的数组了。
我们不妨把把每个元素当做一个人的生日来考虑一下吧。假设你是班上新来的一位学生,你的生日在 三月 的某一天,你想知道班上是否有人生日跟你生日在 t=30 天以内。在这里我们先假设每个月都是30天,很明显,我们只需要检查所有生日在 二月,三月,四月 的同学就可以了。
BFS算法模板 宽度优先
/**
* 返回根节点和目标节点之间最短路径的长度。
* BFS是队列, DFS是栈
*/
int BFS(Node root, Node target)
{
Queue<Node> queue; // 存储所有等待处理的节点
int step = 0; // 从根节点到当前节点需要的步骤数
// 初始化节点
queue.Enqueue(root);
// BFS
while (queue.Count != 0)
{
step = step + 1;
// 迭代队列中已经存在的节点
int size = queue.size();
for (int i = 0; i < size; ++i)
{
// 出队
Node cur = queue.Dequeue();
// 和目标节点进行逻辑判断
return step if cur is target;
// 将cur的子节点都加入到queue中
for (Node next : the neighbors of cur)
{
add next to queue;
}
//remove the first node from queue;
}
}
return -1; // there is no path from root to target
}
DFS模板 深度优先
boolean DFS(int root, int target)
{
// 已访问过的节点
Set<Node> visited;
// DFS用的栈
Stack<Node> stack;
add root to stack;
while (stack.Count != 0)
{
Node cur = stack.Peek();
return true if cur is target;
for (Node next : the neighbors of cur)
{
if (next is not in visited)
{
stack.Push(next);
visited.Add(next);
}
}
stack.Pop();
}
return false;
}
查并集
话说江湖上散落着各式各样的大侠,有上千个之多。他们没有什么正当职业,整天背着剑在外面走来走去,碰到和自己不是一路人的,就免不了要打一架。但大侠们有一个优点就是讲义气,绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”,只要是能通过朋友关系串联起来的,不管拐了多少个弯,都认为是自己人。这样一来,江湖上就形成了一个一个的帮派,通过两两之间的朋友关系串联起来。而不在同一个帮派的人,无论如何都无法通过朋友关系连起来,于是就可以放心往死了打。
但是两个原本互不相识的人,如何判断是否属于一个朋友圈呢?
我们可以在每个朋友圈内推举出一个比较有名望的人,作为该圈子的代表人物。这样,每个圈子就可以这样命名“中国同胞队”美国同胞队”……两人只要互相确认一下自己的队长是不是同一个人,就可以确定敌友关系了。
但是还有问题,大侠们只知道自己直接的朋友是谁,很多人压根就不认识队长要判断自己的队长是谁,只能漫无目的的通过朋友的朋友关系问下去:“你是不是队长?你是不是队长?”这样,想打一架得先问个几十年,饿都饿死了,受不了。这样一来,队长面子上也挂不住了,不仅效率太低,还有可能陷入无限循环中。于是队长下令,重新组队。队内所有人实行分等级制度,形成树状结构,我队长就是根节点,下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候,只要一层层向上问,直到最高层,就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否是一个帮派的,至于他们是如何通过朋友关系相关联的,以及每个圈子内部的结构是怎样的,甚至队长是谁,都不重要了。所以我们可以放任队长随意重新组队,只要不搞错敌友关系就好了。于是,门派产生了。
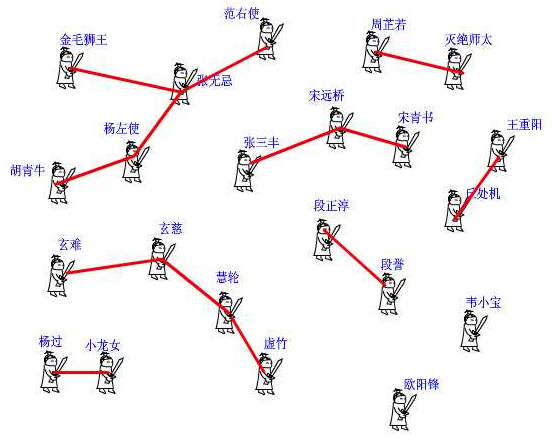
如果一个人的上级就是他自己,那说明他就是掌门人了,查找到此为止。也有孤家寡人自成一派的,比如欧阳锋,那么他的上级就是他自己。每个人都只认自己的上级。比如胡青牛同学只知道自己的上级是杨左使。张无忌是谁?不认识!要想知道自己的掌门是谁,只能一级级查上去。
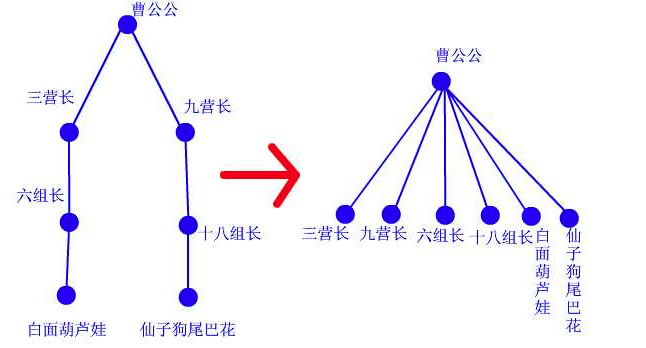
每次一级一级查上去有点费事, 大侠们每次打架前都要问很多次, 因此他们决定如果他们的掌门相同, 就一起结拜在掌门手下, 下次只要问一次就能知道. 这样,查询中所有涉及到的人物都聚集在曹公公的直接领导下。每次查询都做了优化处理,所以整个门派树的层数都会维持在比较低的水平上。路径压缩的代码.
再来看看join函数,就是在两个点之间连一条线,这样一来,原先它们所在的两个板块的所有点就都可以互通了。这在图上很好办,画条线就行了。但我们现在是用并查集来描述武林中的状况的,一共只有一个pre[]数组,该如何实现呢?虚竹帅锅与周芷若MM是我非常喜欢的两个人物,他们的终极boss分别是玄慈方丈和灭绝师太,那明显就是两个阵营了。我不希望他们互相打架,就对他俩说:“你们两位拉拉勾,做好朋友吧。”他们看在我的面子上,同意了。这一同意可非同小可,整个少林和峨眉派的人就不能打架了。这么重大的变化,可如何实现呀,要改动多少地方?
其实非常简单,我对玄慈方丈说:“大师,麻烦你把你的上级改为灭绝师太吧。这样一来,两派原先的所有人员的终极boss都是师太,那还打个球啊!反正我们关心的只是连通性,门派内部的结构不要紧的。”玄慈一听肯定火大了:“我靠,凭什么是我变成她手下呀,怎么不反过来?我抗议!”于是,两人相约一战,杀的是天昏地暗,风云为之变色啊,但是啊,这场战争终究会有胜负,胜者为王。弱者就被吞并了。反正谁加入谁效果是一样的,门派就由两个变成一个了。
// 这个数组,记录了每个大侠的上级是谁。
int pre[1000]; //存放第i个元素的父节点
// 查找根结点
int unionsearch(int root)
{
int son, tmp;
son = root;
// 判断 当前大侠是不是掌门, 一级一级查找
// 最后root就是掌门
while (root != pre[root]) //寻找根结点
root = pre[root];
// 使层级低的大侠直接拜在掌门手下
// 下次查询只要问一次就能知道是否是同一个掌门
while (son != root) //路径压缩
{
tmp = pre[son];
pre[son] = root;
son = tmp;
}
return root;
}
void join(int root1, int root2) //判断是否连通,不连通就合并
{
int x, y;
// 掌门1
x = unionsearch(root1);
// 掌门2
y = unionsearch(root2);
// 两个掌门不同,说明两个大侠的阵营不同
if (x != y) //如果不连通,就把它们所在的连通分支合并
// 谁赢就当对方老大
pre[x] = y;
}
链表的哨兵节点 以及一些技巧
哨兵节点广泛应用于树和链表中,如伪头、伪尾、标记等,它们是纯功能的,通常不保存任何数据,其主要目的是使链表标准化,如使链表永不为空、永不无头、简化插入和删除。
使用多个指针.记录关键节点.
存储当前节点的前一个节点.
